BZOJ3551【ONTAK2010】Peaks加强版 < Kruskal重构树+DFS序+主席树 >

Problem

【ONTAK2010】Peaks加强版

Description

在有座山峰，每座山峰有他的高度。
有些山峰之间有双向道路相连，共条路径，每条路径有一个困难值，这个值越大表示越难走。
现在有组询问，每组询问询问从点开始只经过困难值小于等于的路径所能到达的山峰中第高的山峰，如果无解输出。

Input

第一行三个数。
第二行个数，第个数为。
接下来行，每行个数，表示从到有一条困难值为的双向路径。
接下来行，每行三个数，表示一组询问。
，，，如果则不变。

Output

对于每组询问，输出一个整数表示答案。

Sample Input

10 11 4
1 2 3 4 5 6 7 8 9 10
1 4 4
2 5 3
9 8 2
7 8 10
7 1 4
6 7 1
6 4 8
2 1 5
10 8 10
3 4 7
3 4 6
1 5 2
1 5 6
1 5 8
8 9 2

Sample Output

HINT

，，

标签：Kruskal重构树 DFS序 主席树

Solution

这道题是BZOJ3545【ONTAK2010】Peaks的强制在线版本。
无法离线，则不能只加边不删边，于是无法直接线段树合并。

这里需要引入这一概念。
对于一个图，我们对其构建：
为每条边都设置一个点，点权为该边边权；为每个点（连同边代表的点）一起建立并查集。

找出当前没有尝试过的最小的边，判断其两端点和的连通性
若两端点尚未联通，则将和的祖先用并查集并到边所代表的点上，这时在重构树上加边,
若当前所有原树上的点都在同一个并查集中，则退出，否则返回步骤

下图是一个的例子，其四个性质在下方标注

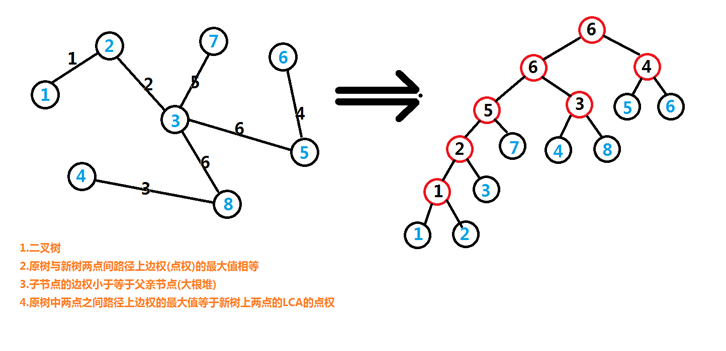
不难发现，由于其是一个大根堆，从一个点出发，只走边权小于等于的点所能到达的点，一定是重构树上一个边所代表的点的子树的所有叶子节点。这样我们在重构树上倍增预处理一下，即可在的时间内找到每个询问对应的上述的这个点。对整棵重构树做树上主席树，即可在的时间内找到第大的点权。

综上，先跑建立重构树，并在重构树上倍增预处理和树上值域主席树预处理。随后对每次询问，先倍增跳到权值小于等于的层数最浅的结点，再在此结点子树的序区间中询问第大权值即可，时间复杂度。

Code

#include <bits/stdc++.h>
#define LOG 20
#define MAX_N 200000
#define MAX_M 500000
#define INF 0x3f3f3f3f
#define mid ((s+t)>>1)
using namespace std;
template <class T> inline void read(T &x) {
    x = 0; int c = getchar(), f = 1;
    for (; !isdigit(c); c = getchar()) if (c == 45) f = -1;
    for (; isdigit(c); c = getchar()) (x *= 10) += f*(c-'0');
}
vector <int> G[MAX_N+5];
int N, M, Q, sz, h[MAX_N+5], fa[MAX_N+5];
int cnt, ind, id[MAX_N+5], into[MAX_N+5], outo[MAX_N+5];
int anc[MAX_N+5][LOG+1], dep[MAX_N+5], rt[MAX_N+5];
int val[MAX_N+5], rev[MAX_N+5], tot; map <int, int> mp;
struct edge {int u, v, c;} E[MAX_M+5];
struct node {int ls, rs, s;} tr[MAX_N*LOG];
void addedge(int u, int v) {G[u].push_back(v);}
bool cmp(const edge &a, const edge &b) {return a.c < b.c;}
int getf(int x) {return fa[x] == x ? x : fa[x] = getf(fa[x]);}
void Kruskal() {
    cnt = 1, sort(E+1, E+M+1, cmp);
    for (int i = 1; i <= N; i++) fa[i] = i;
    for (int i = 1; i <= M && cnt < N; i++) {
        int u = getf(E[i].u), v = getf(E[i].v);
        if (u^v)
            fa[cnt+N] = cnt+N, fa[u] = fa[v] = cnt+N, 
            addedge(cnt+N, u), addedge(cnt+N, v), 
            h[cnt+N] = E[i].c, cnt++;
    }
}
void DFS(int u) {
    into[u] = ++ind, id[ind] = u;
    for (int i = 1; i <= LOG; i++)
        anc[u][i] = anc[anc[u][i-1]][i-1];
    for (int i = 0, v; i < (int)G[u].size(); i++)
        anc[v = G[u][i]][0] = u, dep[v] = dep[u]+1, DFS(v);
    outo[u] = ind;
}
void modify(int v, int o, int s, int t, int p) {
    tr[v] = tr[o]; if (s == t) {tr[v].s++; return;}
    if (p <= mid) modify(tr[v].ls = ++sz, tr[o].ls, s, mid, p);
    if (p >= mid+1) modify(tr[v].rs = ++sz, tr[o].rs, mid+1, t, p);
    tr[v].s = tr[tr[v].ls].s+tr[tr[v].rs].s;
}
int query(int v1, int v2, int s, int t, int k) {
    if (s == t) return s; int rsz = tr[tr[v2].rs].s-tr[tr[v1].rs].s;
    if (k > rsz) return query(tr[v1].ls, tr[v2].ls, s, mid, k-rsz);
    return query(tr[v1].rs, tr[v2].rs, mid+1, t, k);
}
int getpos(int u, int c) {
    for (int i = LOG; ~i; i--)
        if (h[anc[u][i]] <= c) u = anc[u][i];
    return u;
}
int getans(int u, int c, int k) {
    u = getpos(u, c); int l = into[u]-1, r = outo[u];
    if (tr[rt[r]].s-tr[rt[l]].s < k) return -1;
    return rev[query(rt[l], rt[r], 1, N, k)];
}
int main() {
    read(N), read(M), read(Q), h[0] = INF;
    for (int i = 1; i <= N; i++) read(h[i]);
    for (int i = 1; i <= N; i++) val[i] = h[i];
    sort(val+1, val+N+1);
    for (int i = 1; i <= N; i++)
        if (i == 1 || (val[i]^val[i-1]))
            mp[val[i]] = ++tot, rev[tot] = val[i];
    for (int i = 1; i <= N; i++) h[i] = mp[h[i]];
    for (int i = 1, u, v, c; i <= M; i++)
        read(u), read(v), read(c), E[i] = (edge){u, v, c};
    Kruskal(), DFS(getf(1));
    for (int i = 1, p; i < N+N; i++)
        if ((p = id[i]) > N) rt[i] = rt[i-1];
        else modify(rt[i] = ++sz, rt[i-1], 1, N, h[p]);
    for (int i = 1, lst = -1; i <= Q; i++) {
        int u, c, k; read(u), read(c), read(k);
        if (~lst) u ^= lst, c ^= lst, k ^= lst;
        printf("%d\n", lst = getans(u, c, k));
    }
    return 0;
}